« Méthodes de décomposition de domaine pour la formulation mixte duale du problème critique de la diffusion des neutrons »
https://theses.hal.science/tel-00210588
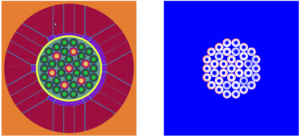
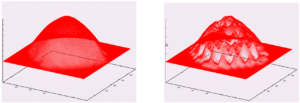
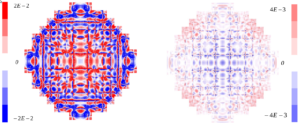
« La simulation de la neutronique d’un cœur de réacteur nucléaire est basée sur l’équation du transport des neutrons, et un calcul de criticité conduit à un problème à valeur propre. Parmi les méthodes de résolution déterministes, l’approximation de la diffusion est souvent utilisée. Le solveur MINOS basé sur une méthode d’éléments finis mixte duale, a montré son efficacité dans la résolution de ce problème. Afin d’exploiter les ordinateurs parallèles, et de réduire les coûts en temps de calcul et en mémoire, nous proposons dans ce mémoire deux méthodes de décomposition de domaine pour la résolution du problème à valeur propre de la diffusion des neutrons sous forme mixte duale. La première méthode est inspirée d’une méthode de synthèse modale : la solution est cherchée dans une base constituée d’un nombre fini de modes propres locaux calculés par MINOS sur des sous-domaines recouvrants. La deuxième méthode est un algorithme itératif de Schwarz modifié qui utilise des sous-domaines non recouvrants et des conditions de Robin aux interfaces entre sous-domaines. A chaque itération, le problème est résolu par MINOS sur chaque sous-domaine avec des conditions aux interfaces calculées à partir des solutions sur les sous-domaines adjacents à l’itération précédente. Les itérations permettent la convergence simultanée de la décomposition de domaine et du problème à valeur propre. Les résultats numériques obtenus sur des modèles 2D et 3D de cœurs réalistes montrent la précision et l’efficacité en parallèle de ces deux méthodes. »
Pierre Guérin